数学模型是什么?为了符合自身数据设置趋势,研发人员会以实验为依据,开发多种数学模型。数学模型是“最佳拟合”线,可用于定性特定测试的数据,具有数据储存便捷的优点,可通过查看斜率和y轴截距对类似测试进行比较。
有一些简单模型可为许多数据设置提供合理拟合,具有一些对多种实践人员(研究人员、质保/质控人员或工艺工程师)有特定含义的参数。在其他事项中,例如,改进后的卡森模型对于测试巧克力效果很好。Herschel-Bulkley模型对于测试具有屈服后屈服点和“剪切稀化”的物料非常有用。比如,这可能很适合测量“凝胶状”物料。
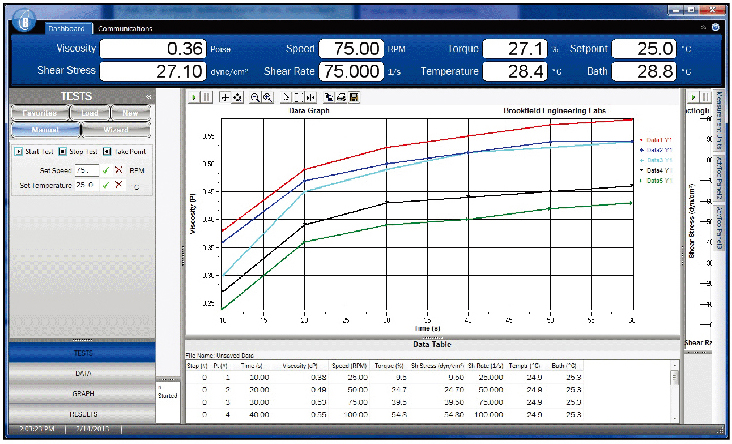
博勒飞RheocalcT软件上运行的数学模型
在我们应用软件(Rheocalc和Wingather)中的博勒飞“分析”模式,列出了曲线拟合参数结果以及“拟合系数”。用户可尝试使用几种模型,并选择具有最佳“拟合系数”的模型,例如-越接近"1.00”,则拟合越好。精确预测产品特性可能比较艰难。比如,适当使用流变学模型可能对在多种剪切率下插入表观粘度值有益。尽管如此,一些模型可用于推断屈服应力,例如,在剪切率值为零的情况下。采集的数据点越多,拟合就越可靠。RheocalcT软件数学模型有: Bingham, Casson, Casson NCa/cma, Power law, PC Paste, Herschel-Bulkley, Thix Index。
也请记住某个模型可能已被使用,因为它“简单”并且“对合理估值足够好”。但并不表示它就是最佳使用模型。石油行业中的一个例子:用Bingham模型检测钻井泥浆流变学特性已有数年,尽管事实是此类物料明显为非牛顿流体!Bingham模型可假设屈服后牛顿流体特性。尽管如此,现场人员认为它在阐明图和处理物料方面“足够好”。在过去几年中,更多实践人员已开始使用"H-B”模型。
关于数学模型及其应用的其他观点:数学模型其实可以看做是一系列规律的总结,对于每一个具体的案例来说,通过配合各种案例下的特殊参数,可以展示出较为相似的数据图表,从而可以节省大量的时间去总结和分析,是一种较为有效的模仿方法。我们在对一个介质进行粘度的测试时,可以通过比较多个数学模型,从而选出最为合适的模型进行
粘度计测试应用。当然,如果对这个介质的数学模型的应用中,有更好的方法去修正这个模型,即改进这个数学模型,那是最好不过的了。
